Question

The x-intercept of the graph of f(x)= 3log(x-5)+2 is:

Answer 1

10^-2/3 +5

Explanation:

Answer 2

Answer:
`\frac{1}{e^{(2)/(3)}}+5` or 5.51

Explanation:

The given function :
`f(x)= 3\log(x-5)+2`

We know that , the x-intercept is the point on graph( basically intersection of graph and x-axis) where y coordinate is zero.

I.e. for x-intercept of function , f(x) =0

i.e.
`0= 3\log(x-5)+2`

`\Rightarrow\ \log(x-5)=(-2)/(3)`

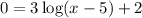
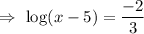
Taking exponent on both sides , we get

`x-5=e^{(-2)/(3)}\\\\\Rightarrow\ x=e^{(-2)/(3)}+5\ \ or\ \ x=\frac{1}{e^{(2)/(3)}}+5`

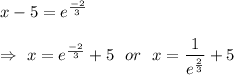
On simplification ,
`\frac{1}{e^{(2)/(3)}}+5\approx5.51`.

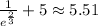Hence , the x-intercept of the graph f(x)=
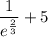`\frac{1}{e^{(2)/(3)}}+5` or 5.51.