To find the zeros of the function

we need to factorize the expression.
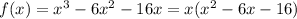
a nice way to factorize
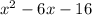
, if possible, is by completing the square as follows:
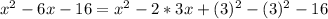
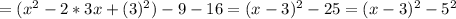
now we use the difference of squares formula
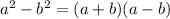
:
![(x-3)^(2)- 5^(2)=[(x-3)+5][(x-3)-5]=[x+2][x-8]](https://img.qammunity.org/2018/formulas/mathematics/high-school/amnoj6yrn7kwu26ipxcdrcfzhk3gqd2hsy.png)
finally, we combine the results:
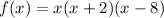
the zeros of f, are the values of x which make f(x)=0,
they are x=0, x=-2 and x=8
Answer: {-2, 0, 8}