Question

The following are the P/E ratios (price of stock divided by projected earnings per share) for 19 banks.

Answer 1

In this problem, we have to compute some percentiles for a data sample. The data sample is:

`18,14,31,34,14,29,50,43,29,20,23,25,22,15,23,18,21,24,19.`

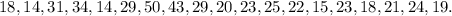
n = number of values = 19.

1) First, we order the data in ascending order:

`14,14,15,18,18,19,20,21,22,23,23,24,25,29,29,31,34,43,50.`

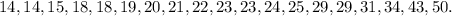
2) We calculate the rank r for the percentile p that we want to find.

`r=(p)/(100)\cdot(n-1)+1.`

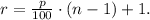
• If r is an integer then the data value at location r, x_r, is the percentile p: p = x_r.

,

• If r is not an integer, p is interpolated using ,ri,, the integer part of r, and, rf,, the fractional part of r:

`P=x_(ri)+r_f\cdot(x_(ri+1)-x_(ri))\text{.}`

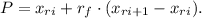
(a) for the 40th percentile, p = 40,

`r=(40)/(100)\cdot(19-1)+1=8.2.`

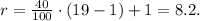
We have r = 8.2, which is not an integer, so we interpolate p using:

• ri = 8,

,

• rf = 0.2,

,

• x_ri = x_8 = 21,

,

• x_(ri + 1) = x_9 = 22.

`P_(40)=21+0.2\cdot(22-21)=21.2.`

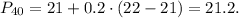
So the 40th percentile is P = 21.2.

(b) for the 75th percentile, p = 75,

`r=(75)/(100)\cdot(19-1)+1=14.5.`

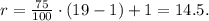
We have r = 14.5, which is not an integer, so we interpolate p using:

• ri = 14

,

• rf = 0.5

,

• x_ri = x_14 = 29

,

• x_(ri + 1) = x_15 = 29

`P_(75)=29+0.5\cdot(29-29)=29.`

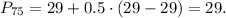
Answers

(a) The 40th percentile: 21 (rounded to the nearest integer)

(b) The 75th percentile: 29