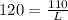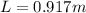Question

The second harmonic of a guitar string has a frequency of 120 hz. what is the length of the guitar string if the speed of the waves on the string is 110 m/s?

Answer 1

L = 0.917 m

Step-by-step explanation:

For nth harmonic of the frequency of the Guitar we can say

`f = (nv)/(2L)`

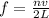
here we know

n = nth harmonics

v = speed of sound in the string of guitar

L = length of the guitar

now from this equation we have

`f = ((2* 110))/(2L)`

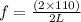
given that

f = 120 Hz

so we have

`120 = (110)/(L)`

`L = 0.917 m`

Answer 2

Frequency, for sound and light waves, is the number of waves that passes per unit of time or the number of complete cycle per unit time. It has units of second^-1 which is equal to 1 Hertz. To determine the length of the guitar string, we simply divide the frequency to the speed of the waves. Speed has units of meter per second. So, dividing frequency would cancel the second unit leaving meters which is a unit of length. We calculate as follows:

Length of string = speed of wave / (frequency)
Length of string = 110 m/s / (120 / s)
Length of string = 0.92 m or 92 cm