it is encouraged to rationalize the denomenator
you can rationalize the denomenator
one way is to convert to exponent
and remember your exponential rules
remember that
![\sqrt[n]{x^m}=x^{(m)/(n)}](https://img.qammunity.org/2018/formulas/mathematics/high-school/lwm9iztoqvnhss9lbouw11pb5txk4y6bqz.png)
also,
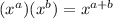
and
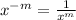
so
![\frac{1}{\sqrt[4]{x^3}}=\frac{1}{x^{(3)/(4)}}](https://img.qammunity.org/2018/formulas/mathematics/high-school/3vhd6hq0vzlsn0bnsuskoo8nvmohj3zde6.png)
so we want x^{4/4}, so 1/4+3/4=4/4
times the whole thing by
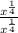
to get
![\frac{x^{(1)/(4)}}{x^{(4)/(4)}}=\frac{x^{(1)/(4)}}{x}=\frac{\sqrt[4]{x}}{x}](https://img.qammunity.org/2018/formulas/mathematics/high-school/pvris37w1zvcfcwyouw3if3a79ph07pdge.png)
but, it looks alot nicer in the original form tho
the 2nd one, we multiply it by
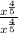
to get
![\frac{x^{(4)/(5)}}{x}=\frac{\sqrt[5]{x^4}}{x}](https://img.qammunity.org/2018/formulas/mathematics/high-school/a37nfpnqhldymzsb55n820n1qjfa0eo7fj.png)
but it looks nicer in original form tho
so you can ratinalize the denomenator but you don't always have to