Question

There are 150 marigold plants in a back yard. Each month, the number of marigold plants decreases by 15%. There are 125 sunflower plants in the back yard. Each month, 8 sunflower plants are removed. Part A: Write functions to represent the number of marigold plants and the number of sunflower plants in the back yard throughout the months. (4 points) Part B: How many marigold plants are in the back yard after 3 months? How many sunflower plants are in the back yard after the same number of months? (2 points) Part C: After approximately how many months is the number of marigold plants and the number of sunflower plants the same? Justify your answer mathematically. (4 points)

Answer 1

If a quantity A is decreased by 15%, it means that what is left is 85% of it.

85%A=
`(85)/(100)A=0.85A`

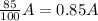
Part A.

Consider the 150 marigolds.

After the first month, 0.85*150 are left
After the second month, 0.85*0.85*150=
`(0.85)^(2) *150`
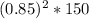
After the third month, 0.85*0.85*0.85*150 =
`(0.85)^(3)*150`
.
.
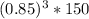
so After n months,
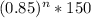
`(0.85)^(n)*150` marigolds are left.

in functional notation:
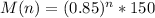
`M(n)=(0.85)^(n)*150` is the function which gives the number of marigolds after n months


consider the 125 sunflowers.

After 1 month, 125-8 are left
After 2 months, 125-8*2 are left
After 3 months, 125-8*3 are left
.
.
After n months, 125-8*n sunflowers are left.

In functional notation: S(n)=125-8*n is the function which gives the number of sunflowers left after n months

Part B.


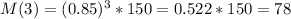
`M(3)=(0.85)^(3)*150=0.522*150=78` marigolds are left after 3 months.

S(3)=125-8*3=125-24=121 sunflowers are left after 3 months.

Part C.

Answer : equalizing M(n) to S(n) produces an equation which is very complicated to solve algebraically.

A much better approach is to graph both functions and see where they intersect.

Another approach is by trial, which gives 14 months


`M(14)=(0.85)^(14)*150=15`


`S(14)=125-8*14=125-112=13`

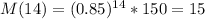
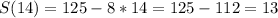
which are close numbers to each other.