Answer: The required length of BC is 32 units.
Step-by-step explanation: Given that the quadrilaterals ABCD and EFGH are similar to each other.
We are to find the length of side BC.
From the figure, we note that
AB = 2x, CD = 3x - 3, EF = 5.5, FG = 8, GH = 7.5 and EH = 7.
Since the corresponding sides of similar figures are proportional, so we get
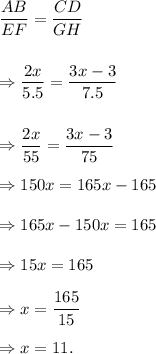
Also, we can write

Thus, the required length of BC is 32 units.