Question

z varies directly as x and inversely as y? If z = 51 when x = 36 and y = 3, find z if x = 25 and y = 7. (Round off your answer tothe nearest hundredth.)

Answer 1

15.18

Step-by-step explanation

If z varies directly as x, then the relationship between them is,

`z=kx`

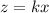
But z also varies directly has y, so the relationship between z and these two variables is,

`z=k\cdot(x)/(y)`

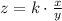
We have to find k, knowing that z = 51 when x = 36 and y = 3,

`\begin{gathered} 51=k\cdot(36)/(3) \\ \\ 51=k\cdot12 \end{gathered}`

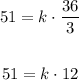
Solving for k,

`k=(51)/(12)=(17)/(4)`

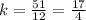
Thus, the relationship is,

`z=(17)/(4)\cdot(x)/(y)`

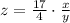
Now, if x = 25 and y = 7, then z is,

`z=(17)/(4)\cdot(25)/(7)=(425)/(28)\approx15.18`

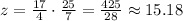
Hence, the value of z when x = 25 and y = 7 is 15.18, rounded to the nearest hundredth.