Question

Given the exponential equation 2x = 128, what is the logarithmic form of the equation in base 10?

Answer 1

`2^(x) = 128`

`log_2 128 = x`

`x = (log_(10)128)/(log_(10)2)`

Answer 2

`log_(2)128= (log_(10) 128)/(log_(10) 2)`.

Explanation:

Given :
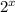`2^(x)` = 128.

To find : what is the logarithmic form of the equation in base 10

Solution : We have given that
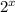`2^(x)` = 128.

By th change base rule ( inverse of exponential function )

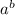`a^(b)` = c is equal to
`log_(a)(c)` = b

Then
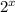`2^(x)` = 128 in to logarithm form
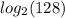`log_(2)(128)` = x.

Then in to the base 10 logarithmic form.

By the change of base formula
`log_(b)a= (log_(10) a)/(log_(10) b)`.

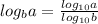Then ,
`log_(2)128= (log_(10) 128)/(log_(10) 2)`.

Therefore,
`log_(2)128= (log_(10) 128)/(log_(10) 2)`.