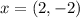Question

4x^2 -16=0 factoring

Answer 1

The given equation is

`4x^2-16=0`

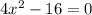
We will factor the given equation using the difference of squares formula given below

`a^2-b^2=(a+b)\cdot(a-b)`

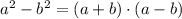
So, we have

`a=2x,b=4`

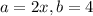
Applying the above formula will result in,

`\begin{gathered} a^2-b^2=(a+b)\cdot(a-b) \\ (2x)^2-(4)^2=(2x+4)\cdot(2x-4) \end{gathered}`

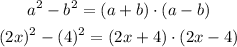
Therefore, the factors of the given equation are

`(2x+4)\text{ and }\left(2x-4\right)`

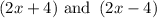
Bonus:

You can find the possible values of x by equating the factors to zero.

`\begin{gathered} (2x+4)=0 \\ 2x=-4 \\ x=-(4)/(2) \\ x=-2 \end{gathered}`

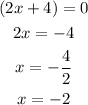
Similarly,

`\begin{gathered} (2x-4)=0 \\ 2x=4 \\ x=(4)/(2) \\ x=2 \end{gathered}`

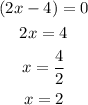
So, the possible values of x are

`x=(2,-2)`