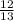Question

In the triangle below, what ratio is sin θ? right triangle with sides whose lengths are 5, 12, and 13; angle theta is opposite the side whose length is 12

Answer 1

If you sketch the triangle, you need to understand that 12 is the length of opposite side (opposite to theta). Then the longest side is 13 is the hypotenuse. The other side with length 5 is the adjacent side. Thus from the definition of sin(theta)=opposite side/hypotenuse=12/13. A question for you, what is cos(theta)? cos(theta)=5/15 and tan(theta)=12/5

Answer 2

Sin θ =
`(12)/(13)`

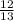
Explanation:

In the figure attached, ABC is a right angle triangle.

Sides of this triangle are AB = 12 BC = 5 and CA = 13

Angle opposite to the side having length = 12 is θ.

Now we have to calculate sin θ.

Since Sinθ =
`\frac{\tex{Opposite side}}{\tex{Hypotenuse}}`

=
`(12)/(13)`

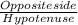
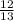
Therefore, ratio which represents sinθ will be
`(12)/(13)`