Answer:
Domain-- All the real numbers.
Range-- [4,∞)
Explanation:
We are given a function f(x) as:
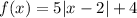
We know that domain of a function is the set of all the x-values where the function is well defined.
Also, we know that the modulus function is defined for all the real numbers and hence adding a constant does not change the domain of the function.
Hence, Domain of function is all the real numbers.
Also, we know that:
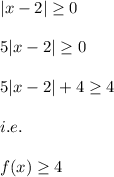
Hence, the Range is the set of all the real values greater than or equal to 4.
Hence,
Range= [4,∞)