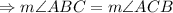Question

Please help.

The octagon in the figure is equiangular and AB ≈ AC  .
Find m<ACB
A. 135
B. 45
C. 30
D. 90
PLEASE SHOW YOUR WORK.

Answer 1

The sum of the measures of the interior angles of a regular octagon equal 1080. Each angle equals 1080/8 = 135
The interior angle B = 135 so it's supplement (angle ABC) = 45 degrees. Since AB = AC, triangle ABC is isosceles, therefore angle ACB also equals 45 degrees.
Letter B

Answer 2

`\boxed{\boxed{m\angle ACB=45^(\circ)}}`

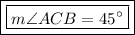
Solution-

The octagon in the figure is equiangular, i.e the octagon is a regular octagon.

So the octagon has 8 equal sides and 8 equal interior angles.

The sum of all of the interior angles is
`(n-2)180=6* 180=1080^(\circ)`

Measurement of each interior angle is,

`(1080)/(8)=135^(\circ)`

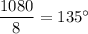
∠ABC is the exterior angle of the octagon.

The interior and exterior angles are complimentary, so

`\Rightarrow 135^(\circ)+m\angle ABC=180^(\circ)`

`\Rightarrow m\angle ABC=180^(\circ)-135^(\circ)`

`\Rightarrow m\angle ABC=45^(\circ)`

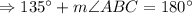
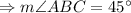
As, in ΔABC AB = AC, so

`\Rightarrow m\angle ABC=m\angle ACB`

`\Rightarrow m\angle ABC=m\angle ACB=45^(\circ)`