The balanced equation is

We need the molar mass of each compound.
• The molar mass of Hg(NO3)2 is 324.7 g/mol.
,
• The molar mass of Na2Cr2O7 is 261.97 g/mol.
,
• The molar mass of HgCr2O7 is 416.58 g/mol.
,
• The molar mass of 2Na(NO3) is 169.99 g/mol.
Then, we find the number of moles of each reactant.
• Moles of Hg(NO3)2 = 24.68g ÷ 324.7 g/mol = 0.076 mol.
,
• Moles of Na2Cr2O7 = 7.41g ÷ 261.97 g/mol = 0.028 mol.
According to equation 1 mole of Hg(NO3)2 will react with 1 mole of Na2Cr2O7, which means 0.076 mol of Hg(NO3)2 has to react with 0.076 mol Na2Cr2O7, which is not possible because there are not enough moles to get 0.076 of Na2Cr2O7 in the reaction. Hence, Na2Cr2O7 is the limiting reactant and Hg(NO3)2 is the excess reactant.
Then, subtract the number of moles to obtain the excess:
The remaining moles from Hg(NO3)2 are: 0.076mol - 0.028 = 0.048 mol.
Therefore, the remaining excess reactant is 0.048 moles.
But, we need to transform it to grams using the molar mass of Hg(NO3)2.
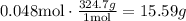
Therefore, the remaining mass of Hg(NO3)2. is 15.59 grams.