Question

Below are two different functions, f(x) and g(x). What can be determined about their slopes?

f(x)= 3x − 3

The function g(x) going through 0, 2 and 1, 5


The function f(x) has a larger slope.
The function g(x) has a larger slope.
They both have the same slope.
The relationship between slopes cannot be determined.

Answer 1

Let's find the slope of the line through (0,2) and (1,5)

m = (y2 - y1)/(x2 - x1)
m = (5-2)/(1-0)
m = 3/1
m = 3

So the slope of g(x) is 3. The slope of f(x) is also 3. The two functions have the same slope.

Answer 2

C. They both have the same slope.

Explanation:

We have the function f(x) = 3x-3.

Substituting values of x in above f(x), we get the pair of points (0,-3) and (1,0).

Now, we will find the slope m of this function using,

`m = (y_(2) -y_(1) )/(x_(2)- x_(1) )`

i.e.
`m = (0 - (-3))/(1-0)`

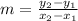
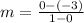
i.e. m = 3.

Now, we are given that the function g(x) passes through the points (0,2) and (1,5).

We will find the slope of g(x) also by using the formula above,

i.e.
`m = (5 - 2)/(1-0)`

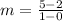
i.e. m = 3.

Hence, we can see that both f(x) and g(x) have slope 3.

So, they both have same slope.