Question

A parabola can be represented by the equation x2 = 2y. What are the coordinates of the focus and the equation of the directrix? focus: (0,8); directrix: y = –8 focus: ; directrix: y = focus: (8,0); directrix: x = –8 focus: ; directrix: x =

Answer 1

the second is the answer i think sorry if im wrong 

Answer 2

Hence, corresponding to the equation of the parabola as: x^2=2y we get:

Focus : (0,0.5)

Directrix : y= -1/2 or y= -0.5

Explanation:

We are given a equation of parabola as:

`x^2=2y`

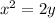
We know that for any The standard form of parabola is:

(x-h)^2=4p×(y-k), where the focus is (h,k+p) and the directrix is y=k-p.

so on comparing the equation with the general equation of the parabola:

`(x-0)^2=2(y-0)`

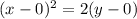
we have:

h=0, k=0.

and
`4p=2\\\\p=(1)/(2)`

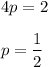
Hence, focus of the parabola is:

(0,0+1/2)=(0,1/2)=(0,0.5)

and directrix equation is given by:

y=0-1/2

y= -1/2

⇒ y= -0.5.

Hence, corresponding to the equation of the parabola as: x^2=2y we get:

Focus : (0,0.5)

Directrix : y= -1/2 or y= -0.5