Question

How many pounds of peanuts costing $1.90/Ib and raisins costing $2.50/Ib should Mr. Bruckner mix to make 12 Ib of a trail mix that costs $2.05/ib

Answer 1

Let p and r be the amount of peanuts and raisins respectively.

p+r=12, p=12-r

We are given that:

(1.9p+2.5r)/12=2.05, using p found above in this equation:

(1.9(12-r)+2.5r)/12=2.05 perform indicated multiplication on left side

(22.8-1.9r+2.5r)/12=2.05 combine like terms on left side

(22.8+0.6r)/12=2.05 multiply both sides by 12

22.8+0.6r=24.6 subtract 22.8 from both sides

0.6r=1.8 divide both sides by 0.6

r=3, and since p=12-r

p=12-3

p=9

So Mr. Bruckner will need to mix 9 pounds of peanuts with 3 pounds of raisins to make a 12 pound mixture which costs $2.05 per pound.

Answer 2

Mr. Bruckner should mix 9 pounds of peanuts and 3 pounds of raisins.

Explanation:

Let the amount of peanut to be added in mixture be x lbs.

Let the amount of raisins to be added in mixture be y lbs.

Amount of the mixture = 12 lb

x lbs + y lbs= 12 lbs

x + y = 12...(1)

Cost of peanuts = $1.90/Ib

Cost of raisins = $2.50/Ib

`x* \$1.90/Ib+y* \$2.50/Ib=12 lb* \$2.05/lb`

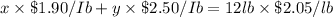
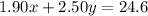`1.90x+2.50y=24.6`..(2)

Solving equation (1) and (2) we get:

x = 9 lbs

y = 3 lbs

Mr. Bruckner should mix 9 pounds of peanuts and 3 pounds of raisins.