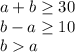Answer:
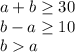
Explanation:
Givens
- The sum of two positive integers is at least 30.
- Their difference is at least 10.
- b is greater than a.
With this information, we can find a system of inequalities. Remember that "at least" means that the sum of these number is 30 or more, and their difference is 10 or more. So
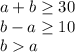
The solution of this system is attached. Remember that the solution of a system of inequalities is a graphic solutions, the intersection of all three areas is the solution.
However, the problem is just asking for the system that could represent this situation. So, the answer is