Question

two debt payments, the first for $800 due today and the second for $600 due in nine months with interest at 10.5% compound monthly, are to be settled by a payment of $800 six months from now and a final payment in 24 months. Determine the size of the final payment if money is now worth 9.5% compounded quarterly.

Answer 1

Given:

First payment = $800 due today

Second payment = $600 in 9 months

Interest rate = 10.5% compounded monthly

The interest is to be settled in a payment of $800 in 6 months and a final payment in 24 months.

Let's determine the final payment if the money is now worth 9.5% compounded quarterly.

Apply the compound interest formula:

`A=P(1+(r)/(n))^(nt)`

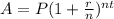
Let x represent the initial amount of debt.

Thus, we have the equation:

`\begin{gathered} (x-800)(1+(0.105)/(12))^{12\ast(9)/(12)}=600 \\ \\ (x-800)(1.00875)^9=600 \\ \\ (x-800)(1.08156)=600 \\ \\ x-800=(600)/(1.08156) \\ \\ x=1340.44 \end{gathered}`

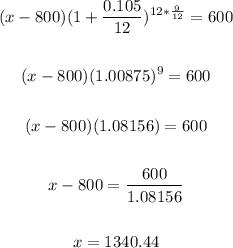
For the amount due in six months, we have:

`\begin{gathered} A=1340.44(1+(0.095)/(4))^{4\ast(6)/(12)}_{} \\ \\ A=1340.44(1.02375)^2 \\ \\ A=1404.87 \end{gathered}`

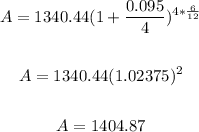
Hence, the amount which is due after 6 months will be:

$1404.87 - $800 = $604.87

Now, let's find the payment due in 24 months.

Number of months remaining = 24 - 6 = 18 months.

Hence, we have:

`\begin{gathered} A=604.87(1+(0.095)/(4))^{4\ast(18)/(12)} \\ \\ A=604.87(1.02375)^6 \\ \\ A=696.35 \end{gathered}`

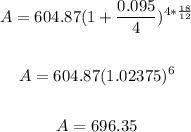
Therefore, the final payment if the money is now worth 9.5% compounded quarterly is $696.35

ANSWER:

$696.35