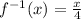Question

Which represents the inverse function of the function f(x)=4x?

Answer 1

we have the function:

f(x)=4x --> y= 4x

To find the inverse we have to change "x" by "y" and "y" by "x", as following:

x=4y

Now, we isolate "y":

Answer 2

The required inverse of the function f(x) is :

`f^(-1)(x)=(x)/(4)`

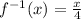
Explanation:

The function is given to be f(x) = 4x

To find the inverse first take f(x) as y and equate it equal to the 4x

Now, let y = 4x

Now, interchange the places of x and y

⇒ x = 4y

Then solve for the value of y and the obtained value of y is the required inverse of the given function f(x)

`(x)/(4)=y\\\\\implies f^(-1)(x)=(x)/(4)`

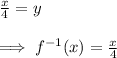
Hence, The required inverse of the function f(x) is :

`f^(-1)(x)=(x)/(4)`