Question

How many values of x must be excluded in the expression (x - 2) / (x + 9) (x - 5) ?

A. 0
B. 1
C. 2
D. 3

Answer 1

C. 2

the 1x in the numerator position would "cancel out" 1 of the x's in the denominator (this description makes more sense if you viewed the entire problem written out as a fraction)

Answer 2

Answer: The correct option is (C). 2.

Step-by-step explanation: We are given to find the number of value of x that must be excluded in the expression below:

`E=(x-2)/((x+9)(x-5)).`

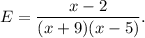
We have to exclude those values of x for which the expression E becomes undefined.

Since E is a rational expression, so the becomes undefined only when the denominator becomes 0.

That is,

`(x+9)(x-5)=0\\\\\Rightarrow x+9=0~~~~~~~~x-5=0\\\\\Rightarrow x=-9,~~~~~~~~\Rightarrow x=5.`

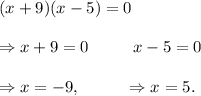
Therefore, we need to exclude the values x = -9 and x =5.

So, there are two values of x to be excluded from the given expression.

Thus, the number of values of x to be excluded is 2.

Option (C) is CORRECT.