Question

The population of a local species of dragonfly can be found using an infinite geometric series where a1 = 30 and the common ratio is 2/5. Write the sum in sigma notation and calculate the sum that will be the upper limit of this population.

Answer 1

The sum will be:

sigma(i = 1 to infinity, 30*(2/5)^i)

->
`\lim_(i \to \infty) (30(1- (2)/(5)^(i) ))/( (3)/(5) )`

Which is equal to 30/(3/5) = 50

Answer 2

50 is the answer.

Explanation:

We have,
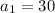`a_(1) =30` and common ratio d=2/5.

So, the general form of the geometric series is
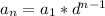`a_(n) =a_(1) *d^(n-1)`, for 'n' is from 1 to infinity.

Hence, the sum in sigma form =
`\sum a_(1) *d^(n-1)`, where n goes from 1 to infinity.

Now, the infinite sum of geometric series =
`(a_(1) )/(1-d)`

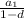
i.e.
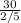`(30)/(2/5)` = 50

Hence, the sum which will be the upper limit is 50