Question

If the radius of a sphere is halved, what happens to the volume of the sphere? Use your algebra skills to develop a formula for the volume of the reduced sphere, V', in terms of V.

Answer 1

Since V = (4/3) * pi * R^3

If R is halved, V' will reduce by a ratio of (1/2)^3 = 1/8

So V' = (1/8)V

Answer 2

Explanation:

Given that the radius of a sphere originally r is halved. We have to find the new volume of the sphere.

Volume of the sphere =
`(4)/(3) \pi r^3`

When radius is halved new radius = r/2

Hence volume of the reduced sphere

=
`(4)/(3)\pi ((r)/(2) )^3=(1)/(8) (4)/(3)\pi r}^3\\=(1)/(8) V`

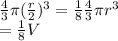
Volume becomes 1/8 times of the original volume.