the perimeter of triangle is equal to the sum of all the side of the triangle,
The perimeter of given triangle is x+y+9+3
Solve for x and y,
Apply pythagoras theorem in triangle ADC,
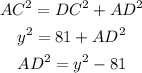
Now, in triangle ADB
Apply pythagoras,
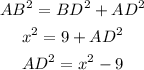
Compare the value of AD from both the equation,
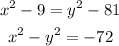
Now, in triangle ABC
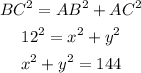
Add the equation
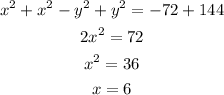
Substitute x=6 in the above equation,
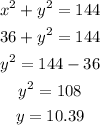
So, the value of the other side of triangle are 6, 10.39
Perimeter of triangle =sum of all sides of triangle
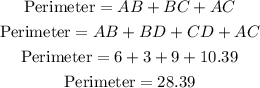
ANSWER : Perimeter is 28.39