Question

The country of Latveria has a population of 11.2 million at the start of 1988, which grows at 4.4% per year.A) Write a recursive equation for the population of Latveria.B) Write an explicit equation for the population of Latveria.C) To the nearest tenth of a million, what is the population of Latveria at the start of 1994.

Answer 1

A) The recursive formula takes into account the previous term. For each term, the next term is expressed in respect to it

Looking at the given scenario, the popularion is increasing by 4.4%. This means that the common ratio is

1 + 4.4/100 = 1.044

Given that the initial population is 11200000, the recaursive formula or equation would be

`\begin{gathered} f_n=\text{ 1.044}f_{n\text{ - 1}} \\ \text{where f}_1=\text{ 11200000} \end{gathered}`

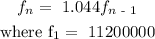
B) For the explicit formula, the general formula for a geometric sequence is

an = a1 * r^(n - 1)

a1 = first term = 11200000

r = common ratio = 1.044

The explicit equation would be

an = 11200000 * 1.044^(n - 1)

C) At the start of 1994, the number of terms, n = 7

We would find a7 by substituting n = 7 into the explicit equation. We have

a7 = 11200000 * 1.044^(7 - 1)

a7 = 11200000 * 1.044^6 = 14501770