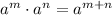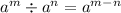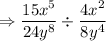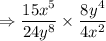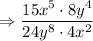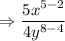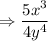Answer:
Simplified form:
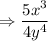
Explanation:
Given: Phrase " 15 x to the fifth power over 24 y to the eighth power divided by 4 x squared over 8 y to the fourth power"
Numerator: "15 x to the fifth power over 24 y to the eighth power"
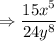
Denominator: "4 x squared over 8 y to the fourth power"
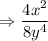
Now we simplify numerator and denominator using exponent law.
Exponent Law: