Question

which recursive formula can be used to generate the sequence shown, where f(1)=5 and n is greater than or less than 1? 5,-1,-7,-13,-19...

Answer 1

f(1) = 5
f(n+1) = f(n) - 6

Answer 2

Answer:
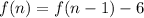`f(n)=f(n-1)-6` , where f(1)=5 and n>1.

Explanation:

The given sequence : 5,-1,-7,-13,-19...

The first term: f(1)=5

We can see that the common difference between each term : d= -6 [-1-5=-6, -7-(-1)=-6, ...]

It mean its arithmetic sequence .

Recursive formula for arithmetic sequence :

`f(n)=f(n-1)+d`

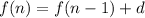
Put d= -6 , we get

`f(n)=f(n-1)+(-6)\\\\ f(n)=f(n-1)-6`

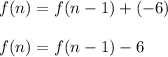
i.e. Recursive formula can be used to generate the given sequence:

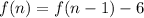`f(n)=f(n-1)-6` , where f(1)=5 and n>1.