If the point (x, y) is dilated about the origin by a scale factor of k, then its image will be (k x, k y), which means we will multiply each coordinate by the scale factor.
Since the vertices of the quadrilateral PQRS are
P = (0, -4)
Q = (8, -4)
R = (8, -8)
S = (0, -8)
Since the scale factor of dilation is 1/4, then
Multiply the coordinates of each point by 1/4 to find the image of it.
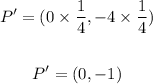
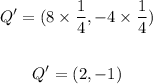
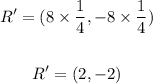
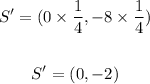
Now, we can graph them