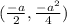Question

Write the quadratic function y = x2 + ax (assuming a is nonzero) in vertex form.

Answer 1

get into form y=a(x-h)²+k where (h,k) is vertex

some terms:
quadratic coefient: number in front of the x² term
linear coefient: number in front of the x term

basically complete the square
so
y=x²+ax
first factor out the quadratic coefient (1),
y=1(x²+ax)
take 1/2 of the linear coefient and square it

`(a)/(2)=(a)/(2)`,
`((a)/(2))^2=(a^2)/(4)`
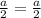
add positive and negative of it inside the parentesees

`y=1(x^2+ax+(a^2)/(4)-(a^2)/(4))`
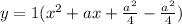
factor perfect square

`y=1((x+(a)/(2))^2-(a^2)/(4))`
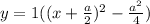
distribute

`y=1(x+(a)/(2))^2-(a^2)/(4)`


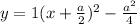
so invertex form, it is

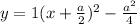
`y=1(x+(a)/(2))^2-(a^2)/(4)` or
the vertex is
`((-a)/(2),(-a^2)/(4))`