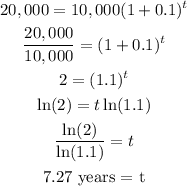Question

Jaryssa invested $10,000 in a construction fund paying 10% return every year. Jaryssaconsidered 2 options for her investment:1) collecting the return every year.2) re-invest all the returns in the same fund.John claimed that after 7 years, Jaryssa will end up with the same amount of money from thisinvestment, while Lary strongly disagreed.a) Calculate how much money would Jarrysa receive from this investment for both options. (Netof her initial $10,000)b) Write a function to represent the value of Jarrysa's investment under each optionc) Graph the 2 functions using the same grid in part b)d) When would the 2 options give her the same return? Be sure to justify your answer.e) How long would it take for Jaryssa to have 20,000 under each plan

Answer 1

a) In option 1, Jaryssa earns 10% of $10,000 each year, that is 10,000*10% = $1,000. Then, after 7 years she will earn 1,000*7 = $7,000.

In option 2, after the first year, she will also earn $1,000 (the 10% of $10,000), but after the second year, she will earn 10% of $11,000 (her cumulative return so far), that is, $11,000*10% = $1,100, so by this time she will have $11,000 + $1,100 = $12,100.

The final amount after the first year can be calculated as $10,000*110% = $11,000.

The final amount after the second year can be calculated as $11,000*110% = $10,000*110%*110% = $10,000*(110%)^2 = $12,100

Therefore, after seven years, there will be $10,000*(110%)^7 = $19,487.17 in her account. This is equivalent to a return of $19,487.17 - $10,000 = $9,487.17.

b) The variable t represents time in years and A the final amount in the account.

In option 1, the function is:

A = 10,000(1 + 0.1t)

Note that multiplying by 0.1 is equivalent to compute the 10% of an amount.

In option 2, the function is:

`A=10,000(1+0.1)^t`

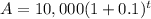
c) In option 1, we have the equation of a line. Two points on this line are (0, 10000) and (1, 11000). Connecting these points with a line we can graph the line.

In option 2, we have an exponential growth function. Three points on this line are (0, 10000), (1, 11000), and (2, 12100). Connecting these points we can graph the function.

d) They will have the same return after the first year.

e) Substituting with A = 20,000 into the equation 1, we get:

20,000 = 10,000(1 + 0.1t)

20,000/10,000 = 1 + 0.1t

2 - 1 = 0.1t

1/0.1 = t

10 years = t

Substituting with A = 20,000 into the equation 2, we get:

`\begin{gathered} 20,000=10,000(1+0.1)^t \\ (20,000)/(10,000)=(1+0.1)^t \\ 2=(1.1)^t \\ \ln (2)=t\ln (1.1) \\ (\ln (2))/(\ln (1.1))=t \\ 7.27\text{ years = t} \end{gathered}`