Question

What is the equation of the quadratic graph with a focus of (4,0) and a directrix of y=10?

Answer 1

The answer is A. If you plug the focus and the directrix into a graph and find the focal length and plug it into the 1/4(a) equation you get 1/20 then plug in the h and the k from the vertex and its negative because the directrix is above the focus and vertex.



A. F(x) = -1/20 (x-4)^2+5

Answer 2

The correct option is 1.

Explanation:

The general equation of a parabola is

`(x-h)^2=4p(y-k)`

Where, (h,k+p) is focus and y=k-p is directrix .

The focus of parabola is (4,0).

`(h,k+p)=(4,0)`

`h=4`

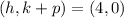
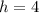
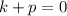`k+p=0` .... (1)

The directrix of parabola is y=10.

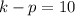`k-p=10` .... (2).

Add equation (1) and (2).

`2k=10`

`k=5`

`p=-5`

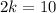
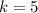
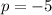
The equation of the parabola is

`(x-4)^2=4(-5)(y-5)`

`(x-4)^2=-20(y-5)`

`-(1)/(20)(x-4)^2=(y-5)`

`-(1)/(20)(x-4)^2+5=y`

`f(x)=-(1)/(20)(x-4)^2+5`

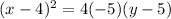
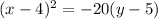
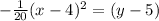
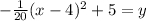
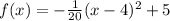
Therefore option 1 is correct.