Question

The surface areas of two similar solids are 384 yd2 and 1057 yd2. the volume of the larger solid is 1795 yd3. what is the volume of the smaller solid?

Answer 1

For similar triangles, the ratio of the corresponding sides are equal. To determine the common ratio, we take the square root of the ratio of the given areas.
ratio = sqrt (384 / 1057)
ratio = 384/1057
Then, for the volume, we have to cube the ratio calculated above. If we let x be the value of the volume of the smaller solid.
(384/1057)^3 = x/1795
x = 86 yd
Thus, the volume of the smaller figure is 86 yd³.

Answer 2

The volume of the smaller solid is approximately 393.051 yd³.

Explanation:

Since, if two solids are similar then the scale factor of similarity is the square root of the ratio of their corresponding surface areas.

Given the surface areas of two similar solids are 384 yd² and 1057 yd²,

Thus,

`\text{Scale factor}=\sqrt{(384)/(1057)}`

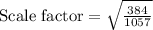
Now, the ratio of volumes of two similar solids is cube of the scalar factor of similarity,

Here, the volume of the larger solid is 1795 yd³,

Let V be the area of the smaller solid,

`\implies (V)/(1795)=(\sqrt{(384)/(1057)})^3\implies V=393.050912175\approx 393.051\text{ Cube yard}`

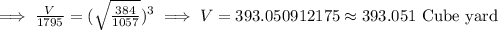
Hence, the volume of the smaller solid is approximately 393.051 yd³.