Question

Check all of the numbers that are potential rational roots of f(x) = x4 – 2x3 + 5x2 – 7x + 9.

a ±1
b ±3
c ±9
d 1/3
e 1/9
f 9/2

Answer 1

a, b, and c

Explanation:

Answer 2

Using Rational root theorem

For any polynomial , ax³ + b x² + c x + d= 0,

To find the possible root , we convert the cubic equation as follows:

⇒
`x^3 +(bx^2)/(a) +(cx)/(a)+(d)/(a)=0`

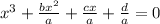
So, the roots will be,
`\pm1, \pm d, \pm (1)/(a),\pm (d)/(a)`.

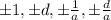Now , the given polynomial having highest degree 4 is :

`f(x) = x^4 - 2x^3 + 5x^2 - 7x + 9.`

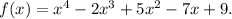
Constant Term =9

So, Possible Roots are = All integral factor of 9=
`\pm 1, \pm 3, \pm 9`

Option (a)
`\pm 1` , Option (b)
`\pm 3` ,and Option (c)
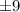`\pm 9` are correct options.