Answer:
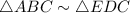
That is, triangles ABC and EDC are similar.
Explanation:
Given :

AE and BD are the common transversal of the parallel lines AB and DE,
Then By the alternative interior angle theorem,
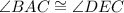
And,
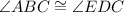
Thus, By AA similarity postulate,
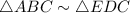
⇒ triangles ABC and EDC are similar.