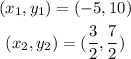Question

I need some help{y=2x^2+6x-10y=-x+5

Answer 1

we are given the following system of equations:

`\begin{gathered} y=2x^{2^{}}+6x-10\text{, (1)} \\ y=-x+5,\text{ (2)} \end{gathered}`

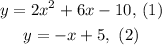
To solve this system of equations we will use the method of substitution by substituting the value of "y" from equation (2) into equation (1), like this:

`-x+5=2x^2+6x-10`

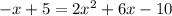
now, we will move all the variables to the right side of the equation by adding "x" on both sides:

`\begin{gathered} -x+x+5=2x^2+6x-10+x \\ 5=2x^2+7x-10 \end{gathered}`

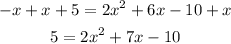
Now we will move the constants to the right side of the equation by subtracting 5 on both sides:

`\begin{gathered} 5-5=2x^2+7x-10-5 \\ 0=2x^2+7x-15 \end{gathered}`

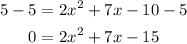
To solve this equation, we will factor the expression on the right side, first by multiplying and dividing by 2

`0=(4x^2+7(2x)-30)/(2)`

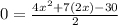
Now we will factor, like this:

`0=((2x+\cdot)(2x-\cdot))/(2)`

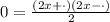
In the spaces, we need to find two numbers which sum is 7 and product are -30, these numbers are 3 and 10, since:

`\begin{gathered} 10-3=-7 \\ (10)(-3)=-30 \end{gathered}`

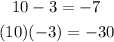
Replacing we get:

`0=((2x+10)(2x-3))/(2)`

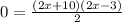
Now we simplify the expression, like this:

`0=(2(x+5)(2x-3))/(2)`
`0=(x+5)(2x-3)`

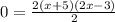
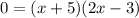
Now, we equal each of the products expressions to zero, like this:

`\begin{gathered} x+5=0 \\ 2x-3=0 \end{gathered}`

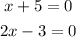
Now we solve for "x" in each one of them:

`\begin{gathered} x_1=-5 \\ x_2=(3)/(2) \end{gathered}`

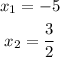
Therefore, the two solutions for "x" are -5 and 3/2. To find the "y" values we replace these values in equation (2). Replacing the first value of "x"

`\begin{gathered} y=-x+5 \\ y=-(-5)+5 \\ y=5+5=10 \end{gathered}`

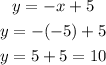
replacing the second value of "x", we get:

`\begin{gathered} y=-x+5 \\ y=-((3)/(2))+5 \\ y=(7)/(2) \end{gathered}`

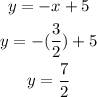
Therefore, the solutions of the system are:

`\begin{gathered} (x_1,y_1)=(-5,10) \\ (x_2,y_2)=((3)/(2),(7)/(2)) \end{gathered}`