Because the random variable X is discrete, the variance of X is defined as
var(X) =
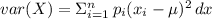
where
p = values of probability as given in the table.
μ = 18.59
Calculate the array (x - μ).
x-μ = [-7.59 -4.59 -2.59 0.41 2.41 4.41 5.41 10.41]
Calculate the array (x-μ)².
(x- μ)² = [57.6081 21.0681 6.7081 0.1681 5.8081 19.4481 29.2681 108.3681]
Calculate the array p*(x-μ)².
p*(x- μ)² = [4.0326 4.4342 1.1404 0.042 0.2904 0.7779 3.8049 8.6694]
Calculate the variance of X.
var(X) = 23.182
Answer:
23.18 (nearest hundredth)