Question

For the past ten years, the population of a city has grown at an annual rate of 2.4% per year. The city’s population in 2020 was 36,314.a.Assuming that the growth rate continues in this fashion, estimate the city’s population in 2025.b.How many years will it take for the city’s population to double at this growth rate?

Answer 1

Let P be the population of the city at any year (t).

Given that the rate of increase of population is 2.4%, so the population in different years is given by,

`\begin{gathered} P_1=1.024\cdot P_0 \\ P_2=1.024^2\cdot P_0 \\ P_3=1.024^3\cdot P_0 \end{gathered}`

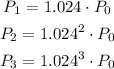
So the general expression representing the population in any nth year is given by,

`P_n=1.024^n\cdot P_0`

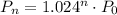
Given that the initial population is 36,314

`P_0=36314`

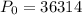
Substitute this value in the general expression,

`P_n=1.024^n\cdot(36314)`

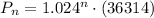
(a)

Note that the year 2020 is considered as the base year (n=0).

So the value of 'n' corresponding to the year 2025 will be,

`\begin{gathered} n=2025-2020 \\ n=5 \end{gathered}`

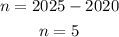
Then, the population in the year 2025 is calculated as,

`\begin{gathered} P_5=1.024^5\cdot(36314) \\ P_5=40885.929 \\ P_5\approx40886 \end{gathered}`

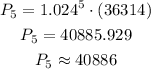
Thus, the city's population will be approximately 40886 in the year 2025.

(b)

Let N be the number of years it takes the population to double itself,

`\begin{gathered} P=2P_0 \\ 1.024^N\cdot P_0=2P_0 \\ 1.024^N=2 \end{gathered}`

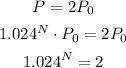
Taking logarithms on both sides,

`\begin{gathered} \ln 1.024^N=\ln 2 \\ N\cdot\ln 1.024=\ln 2 \\ N=(\ln 2)/(\ln 1.024) \\ N=29.226 \end{gathered}`

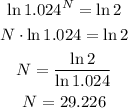
Note that the required number of years is a little more than 29 years, so we have to go for the upper estimate of N, as N cannot be in a fraction.

Therefore, it will take 30 years for the population to double itself.