Question

Can you have a right triangle where the lengths of the legs are whole numbers and the length of the hypotenuse is 23? Explain.

Answer 1

Answer: No,it is not possible to have a right triangle where the lengths of the legs are whole numbers and the length of the hypotenuse is 23.

Explanation:

According to the Pythagorean triplet, in a right angled triangle the hypotenuse is the longest side.

and it is given by
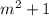`m^2+1` and other two legs are given by
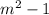`m^2-1` and
`2m`

Now, the longest side=
`m^2+1=23`

`\Rightarrow\ m^2=23-1\\\Rightarrow\ m^2=22`

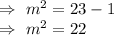
But 22 is not a perfect square

Since
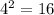`4^2=16` and
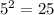`5^2=25`, therefore the square root of 22 lies between 4 and 5.

Hence, it is not possible to have a right triangle where the lengths of the legs are whole numbers and the length of the hypotenuse is 23.