Question

The cost of soup, s, varies directly with the number of cans, c. When c is 4, the cost is 3$. Which graph represents the cost of soup?

Answer 1

s=3/4c since when c=4, s must equal 3

Answer 2

Here,

s represents the cost of soup and c represents the number of can,

Also, s varies directly with c,

⇒ s ∝ c

⇒ s = kc -----(1)

Where, k is the proportionality constant,

Given, when c = 4, s = 3,

From equation (1),

`3=k(4)`

`\implies k=(3)/(4)`

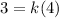
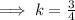
Again from equation (1),

`s=(3)/(4)c`

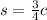
Let x-axis represents the number of can and y-axis represents the cost of soup,

For graphing :

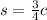`s=(3)/(4)c` is a straight line

Where, s ≥ 0 and c ≥ 0 ( cost and number of cans can not be negative )

When, c = 0, s = 0,

When c = 4,
`s=(3)/(4)* 4=3`

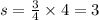
When c = 8,
`s=(3)/(4)* 8=6`

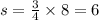
When c = 16,
`s=(3)/(4)* 16=12`

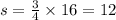
Thus, the line
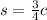`s=(3)/(4)c` is passing from the points (0,0), (4,3), (8,6) and (16,12).