Question

The graph shows the location of Derek's, Evan's, and Frank's houses. Each unit on the graph represents 1 block.

If Frank walks from his house to Derek's house, then on to Evan's house along the path shown, how far will he have walked in blocks? Round your answer to the nearest hundredth.

Answer 1

Crossing a square diagonally is
`√(2)` blocks long.

Frank's to Derek's = 8
`√(2)` blocks

Derek's to Evans = 8 blocks

8 + 8
`√(2 )` = 19.31 blocks

Answer 2

He walked 19.31 unit

Explanation:

By the given table,

The number of blocks between Evan and frank = 8,

Also, the number of blocks between Evan Derek = 8,

Since, the segment joining Derek's and Evan's houses and the segment joining Evan's and Frank's house are perpendicular,

If x represents the number of blocks between Derek's and Frank's house,

Thus, by the pythagoras theorem,

`x^2=8^2+8^2`

`x^2=64+64`

`x^2=128`

`x=√(128)=11.313708499\approx 11.31`

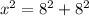
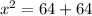
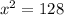
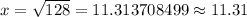
Hence, the total number of blocks in which Frank have walked = Blocks between Derek's and Frank's house + Blocks between Derek's and Evan's house

= 11.31 + 8

= 19.31

Since, each block represents 1 unit,

Therefore, He walked total 19.31 units.