Question

Find the equation of the line described. Write your answer in standard form, perpendicular to the line y=-4/5x-9 and containing (2,-1)

Answer 1

9x - 4y = 22

Step-by-step explanation:

The slope-intercept form of the equation of a line is generally given as;

`y=mx+b`

Where m = slope of the line

b = y-intercept of the line

Given the equation y = -4/5x - 9, we can see that the slope of this line is -4/5.

Any line perpendicular to the given line will have a slope that is a negative reciprocal of the slope of the given line. Therefore the slope of the perpendicular line will be;

`m=(-1)/(-(4)/(9))=-1*(-(9)/(4))=(9)/(4)`

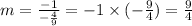
We'll now use the point-slope equation form of the equation of a line to find the required equation of the perpendicular line;

`y-y_1=m(x-x_1)_{}`

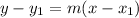
We have m = 9/4 and given the point (2, -1), our x1 = 2 and y1 = -1.

Substituting these values into the point-slope equation, we'll have;

`\begin{gathered} y-(-1)=(9)/(4)(x-2) \\ 4y+4=9x-18 \\ 4y-9x=-18-4 \\ 4y-9x=-22 \\ -9x+4y=-22 \\ 9x-4y=22 \end{gathered}`