Answer:
The slope is m=7
Explanation:
The Slope of a Line
Suppose we have a line that passes through points A(x1,y1) and B(x2,y2). The slope can be calculated with the formula:

We are given the points (3,5) and (4,12), thus: x1=3, y1=5, x2=4, y2=12. Substituting:
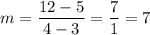
The slope is m=7