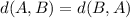Answer:
The length of AB is

Explanation:
Given two points in the plane
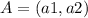 and
and

The distance between this two points is
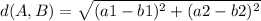 or
or
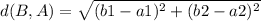
Now for
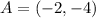 and
and
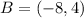
The distance is
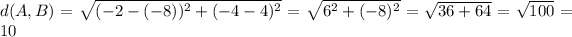
The equation I used derives from operator norm.
Given a point
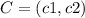 in the plane, the distance between C and (0,0) is
in the plane, the distance between C and (0,0) is
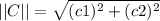
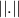 is the operator norm.
is the operator norm.
To find the distance between A and B we apply
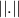 to the diference
to the diference
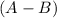 or
or
 in order to obtain the distance equation
in order to obtain the distance equation
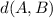 or
or
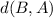
Notice that