Question

1:2-3:When rolling the dice, the outcome is expressed as a sum of the two dice. Forexample, if after you rolled the dice, and one die was a 3 and the other was awill have rolled a 7.4Select all of the TRUE statements below. There may be more than one.The probability of rolling the same digit with each die is 1/4.5The odds in favour of rolling a 10 is 1:13.The odds against rolling a number less than 7 is 7:5.The probability of rolling a number less than 5 is 1.7.

Answer 1

Let X be the random variable representing the sum of the numbers on both the dice.

The random variable can take the values,

`X=\mleft\lbrace2,3,4,5,6,7,8,9,10,11,12\mright\rbrace`

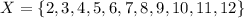
Experiment: Throwing of two six-faced fair dice.

Note that the probability of getting any numbered face on a single dice is 1/6.

Consider the first statement,

`\begin{gathered} P(\text{same number on both dice})=\frac{n\mleft\lbrace(1,1),(2,2),(3,3),(4,4),(5,5),(6,6)\mright\rbrace}{n(\text{Total})} \\ P(\text{same number on both dice})=(6)/(36) \\ P(\text{same number on both dice})=(1)/(6) \end{gathered}`

But the statement claims this probability as 1/4 which is not true.

Therefore, the first statement is false and cannot be marked.

Consider the second statement,

`\begin{gathered} P(X=10)=\frac{n\mleft\lbrace\mleft(4,6\mright),\mleft(5,5\mright),\mleft(6,4\mright)\mright\rbrace}{n(\text{Total})} \\ P(X=10)=(3)/(36) \\ P(X=10)=(1)/(12) \end{gathered}`

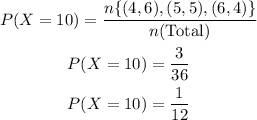
Then the corresponding odds is calculated as,

`\begin{gathered} O(X=10)=(P(X=10))/(1-P(x=10)) \\ O(X=10)=((1)/(12))/(1-(1)/(12)) \\ O(X=10)=(1)/(12-1) \\ O(X=10)=(1)/(11) \end{gathered}`

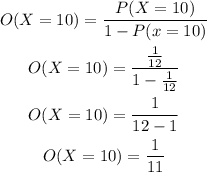
So the odds of getting a sum 10 is obtained as 1/11. But this contradicts with the value given in the statement.

Therefore, the statement is false and cannot be marked.

Consider the third statement,

There are 15 possible combinations that give a sum less than 7,

`\begin{gathered} P(X<7)=(15)/(36) \\ P(X<7)=(5)/(12) \end{gathered}`

The corresponding odds against getting a sum less than 7 is calculated as,

`\begin{gathered} O(X<7)=(1-P(X<7))/(P\mleft(X<7\mright)) \\ O(X<7)=(1-(5)/(12))/((5)/(12)) \\ O(X<7)=(12-5)/(5) \\ O(X<7)=(7)/(5) \end{gathered}`

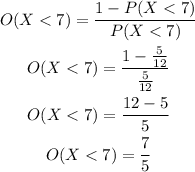
Thus, the odds of getting a sum less than 7 is 7/5. This is the same as given in the statement.

Therefore, the given statement is true and must be marked.

Thus, it can be concluded that only 3rd statement is true and can be marked.