Question

Hi i have put the question in the image please check it

Answer 1

`\begin{gathered} p(\sqrt[]{2})=12\sqrt[]{2}-9 \\ p(-(1)/(2))=2.5 \end{gathered}`

Explanations:

Given the polynomial function

`p(x)=8x^3-6x^2-4x+3`

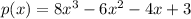
We are to find the equivalent value when x = √2 and x = -1/2

a) Substitute x = √2 into the polynomial function to have:

`\begin{gathered} p(\sqrt[]{2})=8(\sqrt[]{2})^3-6(\sqrt[]{2})^2-4(\sqrt[]{2})+3 \\ p(\sqrt[]{2})=8\lbrack(\sqrt[]{2})^2\cdot\sqrt[]{2}\rbrack-6(2)-4\sqrt[]{2}+3 \\ p(\sqrt[]{2})=8(2\sqrt[]{2})-12-4\sqrt[]{2}+3 \\ p(\sqrt[]{2})=16\sqrt[]{2}-4\sqrt[]{2}-12+3 \\ p(\sqrt[]{2})=12\sqrt[]{2}-9 \end{gathered}`

b) Substitute x = -1/2 into the polynomial function to have:

`\begin{gathered} p(-(1)/(2))=8(-(1)/(2))^3-6(-(1)/(2))^2-4(-(1)/(2))+3 \\ p(-(1)/(2))=\cancel{8}(-\frac{1}{\cancel{8}})-\cancel{6}^3(\frac{1}{\cancel{4}_2})+(4)/(2)+3 \\ p(-(1)/(2))=(-1-(3)/(2))+(2+3) \\ p(-(1)/(2))=-(5)/(2)+5 \\ p(-(1)/(2))=(5)/(2) \\ p(-(1)/(2))=2.5 \end{gathered}`

Therefore the value of the polynomial when x = -1/2 is 2.5