Question

A ship sails for a distance of 150 nautical miles against a current, taking a total of 10 hours. If returns to the starting point, going with the current, in 6 hours. For both trips it moves the same speed through the water. A system of two equations can be used to find the speed of the ship and the current. Let x represent the ship's speed and y represent the speed of the current. What is the correct equation for the ship's return going with the current?

Answer 1

10(x - y) = 150
x- y = 15
y = x - 15

Answer 2

x + y = 25 is the answer.

Explanation:

Let the speed of the ship is represented by x and speed of current by y.

When the ship sails against the current the speed of ship will be (x - y) nautical miles per hour.

Against the current ship sails 150 nautical miles in 10 hours.

So the speed of the ship was =
`\frac{\text{Distance}}{\text{Time}}`

=
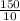`(150)/(10)` nautical miles per hour

And the equation will be (x - y) =
`(150)/(10)=15`

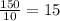
x - y = 15 -------(1)

The same ship when returns with the current then the speed of the ship = (x + y)

Along with the current ship sailed the same distance 150 nautical miles in 6 hours.

Speed of the ship will be =
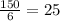`(150)/(6)=25` nautical miles per hour

Now the second equation will be (x + y) = 25 --------(2)

Equation 2 is the equation represents ship's return while going with the current.