A) 16,000
B) 16,400
C) -5 represents that the population will grow after a little decrease
D) P(t) =400t +14000
1) Considering this function:
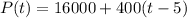
A) Let's start by finding P(5) and P(6), i.e. the number of people when the instant of time (t) is 5 and 6.
So, let's plug that into the function:
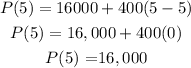
For P(6)
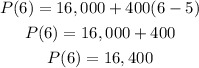
B) If we write the table, we can understand what doest -5 stands for
P(0)= 16,000+400(0-5)= 14000
P(1) = 16,000 +400(1-5)= 14,400
P(2) =16,000+ 400(2-5) = 14,800
(...)
The "t" number of years -5 shows that the population increases after having decreased in comparison to the first years.
C) The factor 400(t-5) represents the growth factor overtime of that population.
D) We need to rewrite that function into the Slope-intercept form:
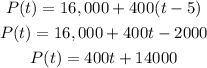
3) Hence, the answer is:
A) 16,000
B) 16,400
C) -5 represents that the population will grow after a little decrease
D) P(t) =400t +14000