Question

Use the method of lagrange multipliers to minimize the function subject to the given constraint. (round your answers to three decimal places.) minimize the function f(x, y) = x2 + 3y2 subject to the constraint x + y ? 1 = 0.

Answer 1

The Lagrangian for this problem is


`L(x,y,\lambda)=x^2+3y^2+\lambda(x+y-1)`

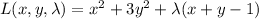
and has partial derivatives


`\begin{cases}L_x=2x+\lambda\\L_y=6y+\lambda\\L_\lambda=x+y-1\end{cases}`

Set each partial derivative equal to 0 and solve for
`x` and
`y`:


`\begin{cases}2x+\lambda=0\\6y+\lambda=0\\x+y=1\end{cases}`

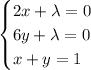
Subtracting the second equation from the first, we get


`2x-6y=0\implies x-3y=0`

and subtracting this from the third equation yields


`4y=1\implies y=\frac14`

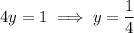
which means


`x+\frac14=1\implies x=\frac34`

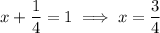
So a critical point occurs at
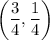
`\left(\frac34,\frac14\right)` (or (0.750, 0.250)). The minimum value would then be
`f\left(\frac34,\frac14\right)=\frac34=0.750`.