Question

Use the divergence theorem to calculate the surface integral s f · ds ; that is, calculate the flux of f across s. (give your answer correct to at least three decimal places.) f(x,y,z) = x3 i + 2xz2 j + 3y2z k s is the surface of the solid bounded by the paraboloid z = 4 ? x2 ? y2 and the xy-plane

Answer 1

`\mathbf F(x,y,z)=x^3\,\mathbf i+2xz^2\,\mathbf j+3y^2z\,\mathbf k`

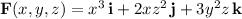
The divergence of the vector field is given by


`\\abla\cdot\mathbf F=(\partial x^3)/(\partial x)+(\partial 2xz^2)/(\partial y)+(\partial 3y^2z)/(\partial z)=3x^2+3y^2`

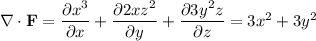
By the divergence theorem, the integral over the surface
`S` is equivalent to the triple integral over the region bounded by
`S` (call it
`R`).


`\displaystyle\iint_S\mathbf F\cdot\mathrm dS=\iiint_R\\abla\cdot\mathbf F\,\mathrm dV`

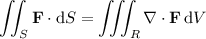
The triple integral can be precisely written as


`\displaystyle\iiint_R\\abla\cdot\mathbf F\,\mathrm dV=3\int_(x=-2)^(x=2)\int_(y=-2)^(y=2)\int_(z=0)^(z=4-x^2-y^2)(x^2+y^2)\,\mathrm dz\,\mathrm dy\,\mathrm dx`

which is easy enough to evaluate directly. You should find that its value is
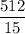
`(512)/(15)`.