Question

The equation of a circle is (x - 3)^2 + (y + 2)^2 = 25. The point (8, -2) is on the circle.

What is the equation of the line that is tangent to the circle at (8, -2)?
y = 8
x = 8
x = 3
y = 3

Answer 1

From the equation, you can see that (3,-2) is the center of the circle (the terms are 0 for those x,y values). The mentioned point has the same y value as the center. That's good news, because it tells us that the tangent line is exactly vertical. The x coordinate is given as x=8. Vertical lines have an equation of x=... so x=8 is the right answer.

Answer 2

Answer: the correct option is

(B) x = 8.

Step-by-step explanation: The given equation of a circle is :

`(x-3)^2+(y+2)^2=25~~~~~~~~~~~~~~~~~~~~~~~~~~~~~(i)`

The point (8, -2) lies on the circle.

We are to select the equation of the line that is tangent to the circle at (8, -2).

We know that

the radius of a circle and the tangent to the circle at the same point of contact are perpendicular to each other.

The STANDARD equation of a circle with center at the point (h, k) and radius of length r units is given by

`(x-h)^2+(y-k)^2=r^2.`

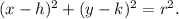
From equation (i), we have

`(x-3)^2+(y+2)^2=25\\\\\Rightarrow (x-3)^2+(y-(-2))^2=5^2.`

So, the center of the circle (i) is (3, -2).

Since the radius of the circle passes through the point (8, -2) and the center (3, -2), so the slope of the radius will be

`m=(-2-(-2))/(3-8)=(0)/(-5)=0.`

So, equation of the radius passing through the point (8, -2) will be

`y-(-2)=m(x-8)\\\\\rightarrow y+2=0\\\\\Rightarrow y=-2.`

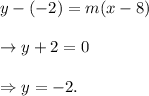
So, the tangent at the point (8, -2) will be of the form

`x=k.`

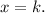
Since the tangent passes through the point (8, -2), so we get

`x=8.`

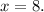
Thus, the required equation of the tangent line at the point (8, -2) is x = 8.

Option (B) is CORRECT.